平成26年東京農工大学編入試験問題解答 力学 ベルトコンベア上の振動
過去問リクエスト。
問題
問題を解く前の予備知識
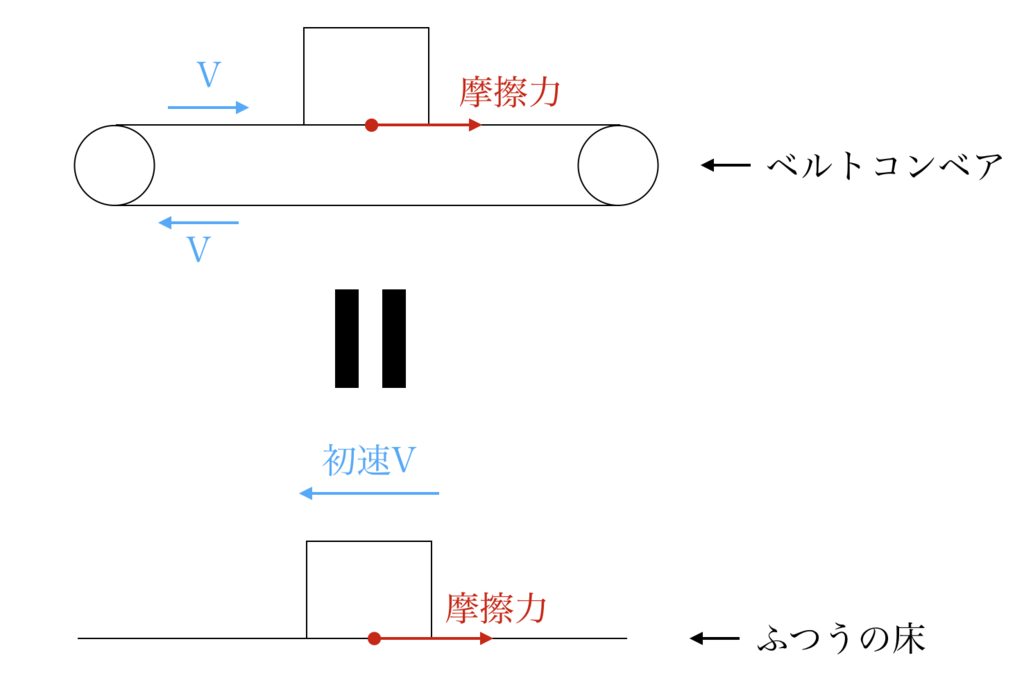
右方向に速度\(V\)で回転するベルトコンベア上を滑る荷物という状況は、観測者がベルトコンベア上にいる場合には、摩擦のある床を初速度\(V\)で左方向に滑る荷物と同じ状況です（摩擦力の向きが一致していることを確認する）
解答
(1) 下図のような初速度\(V\)で動き出した荷物が停止するまでの運動を考えることはとても簡単なので、左方向を正、摩擦力=\(\mu mg\)として\begin{eqnarray}m\frac{d^{2}x}{dt^{2}}&=&-\mu mg\\ \frac{d^{2}x}{dt^{2}}&=&-\mu g\\ \frac{dx}{dt}&=&-\mu gt+V\end{eqnarray}荷物とベルトコンベアの滑りがなくなるまで=速度が\(0\)の時なので\begin{eqnarray}0&=&-\mu gt+V\\ \mu gt&=&V\\t&=&\frac{V}{\mu g}\end{eqnarray}(2) \(x(0)=0\)より\begin{eqnarray}\frac{dx}{dt}&=&-\mu gt+V\\x&=&-\frac{1}{2}\mu gt^{2} + Vt\end{eqnarray}この間\((t=\frac{V}{\mu g})\)に荷物が移動した距離は、\begin{eqnarray}x&=&-\frac{1}{2}\mu g \left(\frac{V}{\mu g}\right)^{2} + V\frac{V}{\mu g}\\&=&\frac{1}{2}\frac{V^{2}}{\mu g}\end{eqnarray}
ばねが自然長の時の位置を\(x=0\)とする。荷物に働く水平方向の力は摩擦力とばねの押し返す力のみで、これらが釣り合う位置を\(x_{0}\)とおくと\begin{eqnarray}\mu mg&=&kx_{0}\\x_{0}&=&\frac{\mu mg}{k}\end{eqnarray}
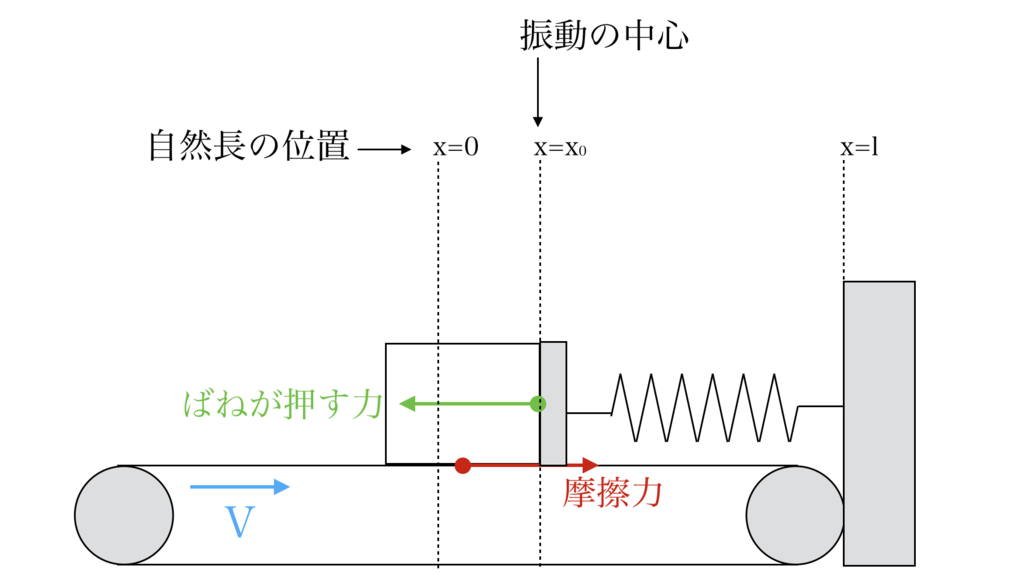
次にこの状況を運動方程式で表すと\begin{eqnarray}m\frac{d^{2}x}{dt^{2}}&=&-kx+\mu mg\\x_{0}&=&\frac{\mu mg}{k}\\\frac{d^{2}x}{dt^{2}}&=&\frac{1}{m}(-kx+\mu mg)\\\frac{d^{2}x}{dt^{2}}&=&-\frac{k}{m}(x-\frac{\mu mg}{k})\end{eqnarray}\(x_{0}=\frac{\mu mg}{k}\)なので\begin{eqnarray}\frac{d^{2}x}{dt^{2}}&=&-\frac{k}{m}(x-x_{0})\end{eqnarray}この時、振動の運動方程式式から、角速度\(\omega\)は\begin{eqnarray}\omega=\sqrt{\frac{k}{m}}\end{eqnarray}よって「(1)周期\(T\)」は\begin{eqnarray}T=\frac{2\pi}{\omega}=2\pi\sqrt{\frac{m}{k}}\end{eqnarray}また、平行移動の式より、\(x_{0}\)は「(2)振動の中心の変位」であることがわかる。よって\begin{eqnarray}x=x_{0}=\frac{\mu mg}{k}\end{eqnarray}振動において、「(3)荷物の速度が最大」になる時はもちろん振動の中心であり、この時運動エネルギー最大、ばねエネルギーは0。 振動の端では逆に運動エネルギー0で、ばねエネルギーは最大。力学的エネルギーが保存することから、\begin{eqnarray}\frac{1}{2}mv^{2}&=&\frac{1}{2}kx_{0}^{2}\\v^{2}&=&\frac{k}{m}x_{0}^{2}\\v&=&x_{0}\sqrt{\frac{k}{m}}\\&=&\frac{\mu mg}{k}\sqrt{\frac{k}{m}}\\&=&\mu g\sqrt{\frac{m}{k}}\end{eqnarray}
まとめ
一見ややこしそうな問題に見えますが、はたらく力が摩擦とばね力しかないので満点が狙えます。2(3)のように運動方程式で解けなければ運動量保存則やエネルギー保存則で解く方針に切り替えるといいと思います。
