平成29年東京農工大学編入試験問題解答 数学 問題2:重積分
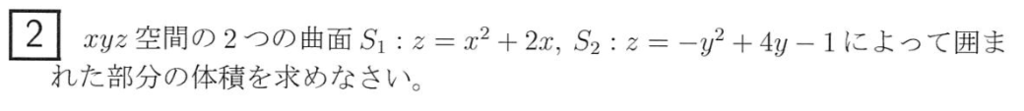
まずは\(x\)と\(y\)の式を平方完成すると
\begin{eqnarray}z=(x-1)^2-1,\ \ z=-(y-2)^2+3\end{eqnarray}
つまり、2つの式の描く曲面は二次関数のように曲がり、それらが直角に重なっていることがイメージできる。

次に積分範囲を定めることで、「\(y\)式の積分-\(x\)式の積分」で容易に体積を求めることができる。
ここでやっかいなのが2つの曲面が重なる線を\(z\)軸方向から見た時に下図のようになり、積分範囲である円の中心が原点にないため、極座標変換が難しくなってしまう。

しかし今回の図を見てもらえばわかる通り、2つの曲面が\((x,y)\)方向に平行移動したところで重なった体積は変化しない。これを利用して2式の\((x,y)\)方向をあらかじめ原点に平行移動しておくと極座標変換が楽になる。つまり\begin{eqnarray}z=(x-1)^{2}-1 \to z=x^{2}-1\\ z=-(y-2)^{2}+3\to z=-y^{2}+3\end{eqnarray}

ここまで来ればあとは「\(y\)式の積分-\(x\)式の積分」を極座標変換して体積を導出する。
ちなみに極座標変換は図を見てもらえば分かると思うが、\(r=4,\theta=2\pi\)
\begin{eqnarray}V&=&\iint_{D}\{(-y^2+3)-(x^2+1)\}dxdy&=&\iint_{D}(4-x^{2}-y^{2})dxdy\\&=&\int_{r=0}^{2}\int_{\theta=0}^{2\pi}(4-r^{2})rdrd\theta\\&=&2\pi\left[2r^{2}-\frac{1}{4}r^{4}\right]_{0}^{2}\\&=&2\pi\left(8-\frac{16}{4}\right)\\&=&8\pi\end{eqnarray}
この問題は何人かの受験生からリクエストされていた問題だったので、難しい部類に入ると思います。重なった曲面の図をきちんとイメージ出来ていれば簡単化することは思いつくと思います。
また、「これよりもっといい方法がある」という場合は、メール等で連絡いただければ助かります。
