平成28年度 東京農工大学編入試験 力学 さまざまな2体運動
先日、農工大の今年度の編入試験の数学を解きました。
続いて力学も解いてみたので、今年度は簡単でしたが参考にどうぞ。
(この過去問は東京農工大学の編入学ページにて無料で入手できます。)
問題と解答
1 滑らかな水平面上で,\(x\)軸政方向に速さ\(v\)で進む質量\(m\)の小球\(A\)が,原点に静止している同じ質量\(m\)の小球\(B\)に一直線上で衝突する問題を考える。2つの小球の反発係数を\(e\)を1とし,小球は大きさが無視できる質点とする。また,衝突は無限小の時間で起こるとする。小問〔6〕以外は答えのみを解答欄に記せ。
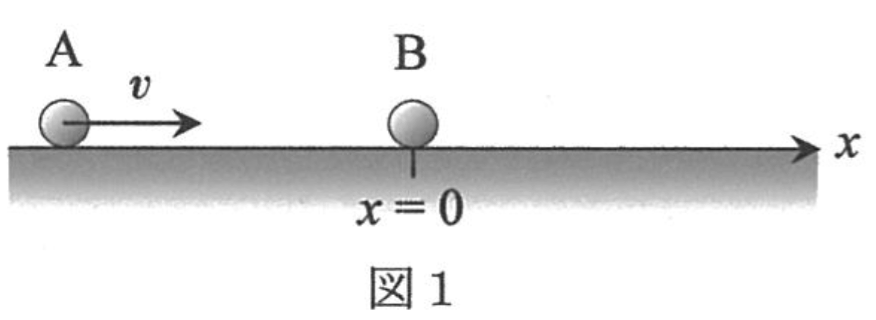
〔1〕図1のように,小球\(B\)が単に原点に置かれている場合を考える。衝突後の小球\(A\) ,\(B\)の速度\(v_{A}\),\(v_{B}\)を求めよ。
〔解答〕
衝突前の小球の速度を\(v_{A}'\),\(v_{B}'\)とすると、それぞれの小球の速度は
\begin{eqnarray}v_{A}'=v,v_{B}'=0\end{eqnarray}
運動量保存則より、
\begin{eqnarray}mv_{A}'+mv_{B}'&=&mv_{A}+mv_{B}\\v&=&v_{A}+v_{B}\tag{1}\end{eqnarray}
さらに跳ね返りの式を立てると
\begin{eqnarray}v_{A}'-v_{B}'&=&e(v_{B}-v_{A})\\v&=&v_{B}-v_{A}\tag{2}\end{eqnarray}
(1)(2)より連立方程式を解いて
\begin{eqnarray}v_{A}=0,v_{B}=v\end{eqnarray}
「滑らかな地面」「\(x\)軸方向」の運動なので、重力などの外力が一切加わらないと考えられます。さらに2つの小球は質量が同じで反発係数1の完全弾性衝突です。ここまで分かっていれば計算もせずに感覚的に\(v_{A}=0\),\(v_{B}=v\)という事がわかってしまうと思います。農工大は計算過程を問わないのでここは単純にショートカットしていきたいですが、他の大学で出題された時のために一応計算過程を示しておきます。
〔2〕小問〔1〕で,2つの小球の運動エネルギーの和\(E\)は衝突の前後でどれだけ変化するか,\(\Delta E=E\)(後)\(-E\)(前)で答えよ。
〔解答〕
衝突前も衝突後も運動エネルギーは\(\frac{1}{2}mv^{2}\)であるため、\(\Delta E=0\)
また、外力が0であることから力学的エネルギーは保存し、\(y\)軸方向への移動がないため、位置エネルギーの変化も0、となると運動エネルギーの変化量も0であることに瞬時に気づいてもらいたいです。
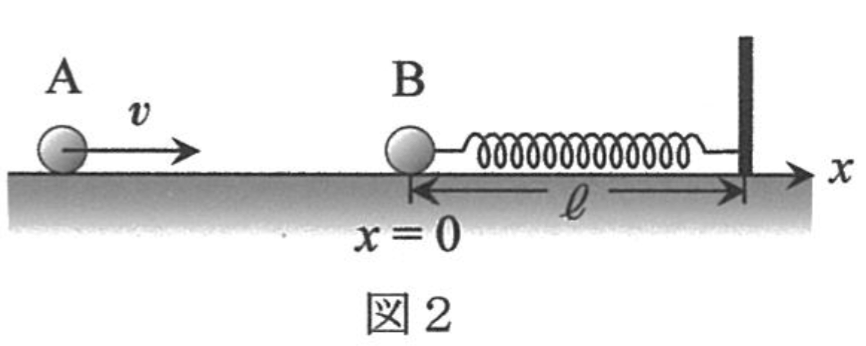
〔3〕図2のように,小球\(B\)にバネ(バネ係数を\(k\)とし,質量を無視する)が自然長\(l\)の状態で取り付けられ,バネの他端が壁に固定されている場合を考える。衝突の瞬間の時刻を\(t=0\)とし,時間を横軸,小球\(A,B\)の位置\(x_{A},x_{B}\)を縦軸にとり,衝突前後の\(x_{A}(t),x_{B}(t)\)の概略のグラフを描け。グラフには,\(t>0\)だけでなく\(t<0\)の領域も含め,特徴的な時刻を記入すること。
〔解答〕
小球\(A\)について考えると,\(t<0\)までは等速運動,\(t=0\)で衝突して静止,再び小球\(B\)に衝突すると逆方向に等速運動します。
また、小球\(B\)については\(t=0\)の時点で初速\(v\)で動き出す単振動である。 小球\(B\)について運動方程式を立てると \begin{eqnarray}m\frac{d^{2}x}{dt^{2}}&=&-kx\\\frac{d^{2}x}{dt^{2}}&=&-\frac{k}{m}x\end{eqnarray}
ここから周期を求めると \begin{eqnarray}\omega &=&\sqrt{\frac{k}{m}}\\T&=&\frac{2\pi}{\omega}\\T&=&2\pi\sqrt{\frac{m}{k}}\end{eqnarray}
図に表すと以下のようになる、


バネがついているものの、この運動は衝突の瞬間の時点では小問〔1〕と同じであることに気づけば簡単に処理できます。またこの問題は小球の動きがわかるような概略がかければいいので、\(x\)の座標は求めず、周期\(T\)を求めるだけで大丈夫でしょう。
〔4〕小問〔3〕でバネが最も縮んだときの長さを求めよ。
〔解答〕
衝突直後の小球\(B\)には運動エネルギーのみ、バネが最も縮む\(v_{B}=0\)の時にはバネのエネルギーのみが存在するので、以上2つの瞬間での力学的エネルギーが保存することから式を立てると
\begin{eqnarray}\frac{1}{2}mv^{2}&=&\frac{1}{2}kx^{2}\\x&=&v\sqrt{\frac{m}{k}}\end{eqnarray}
求めたいのはバネの長さなので、答えは
\begin{eqnarray}l-v\sqrt{\frac{m}{k}}\end{eqnarray}
この問題はバネの運動方程式から\(x\)の振動の式を導き、小問〔3〕で求めた周期\(T\)の\(\frac{1}{4}\)周期を\(t\)に代入しても求める事ができます。しかし時間がかかって計算ミスのおそれもあるので、どちらの方が簡単に解けるかを見極めてください。力学の問題は運動方程式か運動量保存則、力学的エネルギー保存則のどれかのアプローチでほとんど解けます。
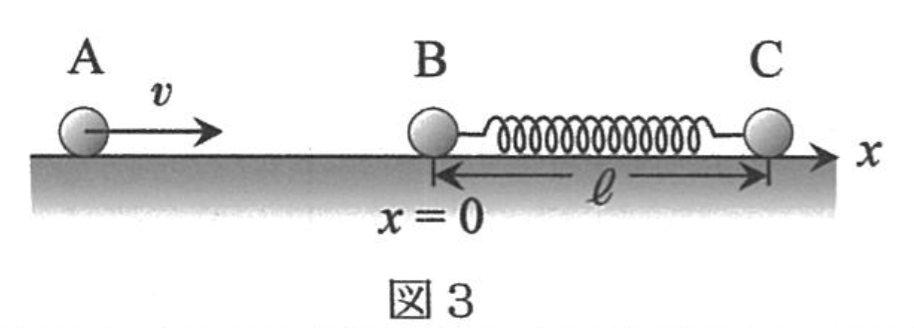
〔5〕図3のように,小球\(B\)にバネが自然長\(l\)の状態で取り付けられ,バネの他端に小球\(A,B\)と同じ質量\(m\)の小球\(C\)が取り付けられている場合を考える。衝突後の小球\(B\)と小球\(C\)の重心(質量中心)の速度を求めよ。
〔解答〕
問題から、初期条件は\(t=0,x=0,v_{B}=v,v_{C}=0\)である。 それぞれの運動方程式は
\begin{eqnarray}m\frac{d^{2}x_{B}}{dt^{2}}&=&-k(l+x_{B}-x_{C})\\m\frac{d^{2}x_{C}}{dt^{2}}&=&k(l+x_{B}-x_{C})\end{eqnarray}
これらを辺々足しあわせて
\begin{eqnarray}m\frac{d^{2}x_{B}}{dt^{2}}+m\frac{d^{2}x_{C}}{dt^{2}}&=&-k(l+x_{B}-x_{C})+k(l+x_{B}-x_{C})\\\frac{d^{2}}{dt^{2}}(mx_{B}+mx_{C})&=&0\end{eqnarray}
両辺に\(\frac{1}{m+m}\)をかけて
\begin{eqnarray}\frac{1}{m+m}\frac{d^{2}}{dt^{2}}(mx_{B}+mx_{C})=0\\\frac{d^{2}}{dt^{2}}(\frac{mx_{B}+mx_{C}}{m+m})=0\\\end{eqnarray}
ここで\(\frac{mx_{B}+mx_{C}}{m+m}\)は重心\(x_{G}\)を表す式であることがわかるので
\begin{eqnarray}\frac{d^{2}x_{G}}{dt^{2}}=0\end{eqnarray}
よってこのバネの重心は加速度0、すなわち等速度運動をする。 ここから重心の速度\(v_{G}\)は
\begin{eqnarray}v_{G}=\frac{dx_{G}}{dt{2}}&=&\frac{d}{dt}(\frac{mx_{B}+mx_{C}}{m+m})\\&=&\frac{1}{2}(\frac{dx_{B}}{dt}+\frac{dx_{C}}{dt})\end{eqnarray}
初期条件\(v_{B}=\frac{dx_{B}}{dt}=v,v_{C}=\frac{dx_{C}}{dt}=0\)から
\begin{eqnarray}v_{G}&=&\frac{1}{2}(v+0)\\&=&\frac{v}{2}\end{eqnarray}
このような運動を特徴的な動きからイモムシ運動といいますが、この問題のキモは最初の運動方程式から重心の運動方程式に変形させる方法だと思います。かなりメジャーな問題なので、式変形できるようにしておきましょう。
〔6〕小問〔5〕で,バネが最も縮んだときの長さを求めよ。答えだけでなく,導出過程を簡潔に記せ。
〔解答〕
問題〔5〕同様にそれぞれの運動方程式は
\begin{eqnarray}m\frac{d^{2}x_{B}}{dt^{2}}&=&-k(l+x_{B}-x_{C})\\m\frac{d^{2}x_{C}}{dt^{2}}&=&k(l+x_{B}-x_{C})\end{eqnarray}
これらを(\(x_{C}\)の式)-(\(x_{B}\)の式)より
\begin{eqnarray}m\frac{d^{2}x_{C}}{dt^{2}}-m\frac{d^{2}x_{B}}{dt^{2}}&=&k(l+x_{B}-x_{C})+k(l+x_{B}-x_{C})\\\frac{d^{2}}{dt^{2}}(x_{C}-x_{B})&=&-\frac{2k}{m}(x_{C}-x_{B}-l)\end{eqnarray}
ここで\(x_{C}-x_{B}\)は「小球\(B\)から見た小球\(C\)との相対距離」である。これを\(X\)とおくと
\begin{eqnarray}\frac{d^{2}X}{dt^{2}}&=&-\frac{2k}{m}(X-l)\end{eqnarray}
これより振動の式であることが分かり、角振動数\(\omega=\sqrt{\frac{2k}{m}}\)であるから、 単振動の式\(\frac{d^{2}}{dt^{2}}(x)=-\omega^{2}(x-x_{0})\)と係数比較して当てはめてみると
\begin{eqnarray}X-l&=&A\cos{\omega t}+B\sin{\omega t}\tag{1}\end{eqnarray}
これを微分して相対速度Vの式は
\begin{eqnarray}V&=&-\omega A\sin{\omega t}+\omega B\cos{\omega t}\tag{2}\end{eqnarray}
\(t=0\)の時点で、\(x_{C}\)は\(x_{B}\)から見ると\(+l\)の位置にあり、相対速度Vとすると、\(x_{B}\)から見ると\(x_{C}\)が速度\(-v\)で近づいてくるように見えるため 初期条件は\(t=0,X=l,V=-v\)
これを式(1),(2)に代入すると\(A=0,\ B=-\frac{v}{\omega}\)
以上から、バネの長さ(相対距離)Xを求める式は
\begin{eqnarray}X&=&-v\sqrt{\frac{m}{2k}}\sin\sqrt{\frac{2k}{m}t}+l\end{eqnarray}
相対距離\(X\)が最小になる時は\(\sin\sqrt{\frac{2k}{m}t}=1\)の時であり すなわち、
\begin{eqnarray}X&=&l-v\sqrt{\frac{m}{2k}}\end{eqnarray}
イモムシ運動は重心の運動と相対距離について問われることが多いです。今回は質量が等しい場合だったので計算しやすかったですが、質量が異なる場合でも面倒なだけで計算できます。
以上で終了です。バネに関する基本的な問題集といった感じがします。編入試験は意外とバネの問題が多い気がするのでこの年度の試験はいい練習になると思います。時間があれば電磁気の方もそのうち解こうと思います。
また、解答が欲しい過去問などありましたらコメント欄などで教えてください。できる範囲で解いてみようと思っています。