平成26年東京農工大学編入試験問題解答 電磁気学 点電荷の電位,電場

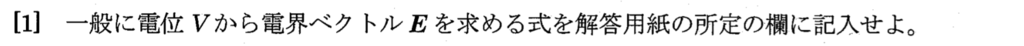
\begin{eqnarray}\bf E \rm=-grad \bf V\end{eqnarray}


\(x\)軸\(y\)軸方向は打ち消しあうので\(z\)軸方向のみ

電位はスカラーなので向きは関係無い。つまり足し合わせることができる。
点\(A\), 点\(B\)の電荷が及ぼす電位をそれぞれ\(V_{A}\),\(V_{B}\)とする。点電荷\(q\)による距離\(r\)の点での電位は\(V=\frac{1}{4\pi\epsilon_{0}}\frac{q}{r}\) であり、距離\(r=\sqrt{z^{2}+a^{2}}\)なので、
\begin{eqnarray}V_{A}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{\sqrt{z^{2}+a^{2}}}, V_{B}=\frac{1}{4\pi\epsilon_{0}}\frac{q}{\sqrt{z^{2}+a^{2}}}\end{eqnarray}
よって \begin{eqnarray}V=V_{A}+V_{B}=\frac{1}{2\pi\epsilon_{0}}\frac{q}{\sqrt{z^{2}+a^{2}}}\end{eqnarray}

[1]の公式通りに、(2)で求めた電位\(V\)を\(x,y,z\)方向についてそれぞれ偏微分すると、
\begin{eqnarray}E_{x}=\frac{\partial V}{\partial x}=0\end{eqnarray} \begin{eqnarray}E_{y}=\frac{\partial V}{\partial y}=0\end{eqnarray} \begin{eqnarray}E_{z}=\frac{\partial V}{\partial z}=\frac{q}{2\pi\epsilon_{0}}\frac{z}{\sqrt{z^{2}+a^{2}}^{3}}\end{eqnarray}

\(E=\frac{q}{2\pi\epsilon_{0}}\frac{z}{\sqrt{z^{2}+a^{2}}^{3}}\)が最大になるとき、つまり\(\frac{z}{\sqrt{z^{2}+a^{2}}^{3}}\)が最大となる時の\(z\)を求めればよいため、極値を求める公式から、
\(f(z)=\frac{z}{\sqrt{z^{2}+a^{2}}^{3}}\)とおき、\(f_{z}=0\)を満たす\(z\)が\(z_{max}\)となる。過程を書くと
\begin{eqnarray}f_{z}=\frac{\sqrt{z^{2}+a^{2}}^{3}-3z^{2}\sqrt{z^{2}+a^{2}}}{(z^{2}+a^{2})^{3}}&=&0\\z^{2}+a^{2}-3z^{2}&=&0\\z&=&\frac{a}{\sqrt{2}}\end{eqnarray}
さいごに\(z_{max}=\frac{a}{\sqrt{2}}\)を\(E\)の解に代入すると\(E_{max}\)が求まる
\begin{eqnarray}E_{max}&=&\frac{q}{2\pi\epsilon_{0}}\frac{z_{max}}{\sqrt{z_{max}^{2}+a^{2}}^{3}}\&=&\frac{q}{2\sqrt{3}\pi\epsilon_{0}}\end{eqnarray}
この問題も基礎物理学演習 (2)で結構かんたんに解けちゃったりします。おわり
